470. Super palindromes
Let us call a
string of length greater than one a palindrome if it
reads the same from left to right and from right to left.
A superpalindrome is a string that can be
represented as a concatenation of one or more palindromes.
Given a string s, find the number of
substrings of s that are
superpalindromes.
Input. One string s (1 ≤ |s| ≤ 1000) consisting of lowercase Latin letters.
Output. Print one
integer – the number of substrings of the string that are
superpalindromes.
|
Sample
input |
Sample
output |
|
abacdc |
3 |
SOLUTION
dynamic programming - palindrome
Algorithm analysis
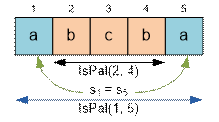
Let s be the input string. A substring si … sj is a palindrome if at
least one of the following conditions is satisfied:
·
i ≥ j, that is, the substring is empty or
consists of a single character;
·
si = sj and the substring si+1…sj-1 is a palindrome;
Let’s define the function IsPal(i, j),
that returns 1 if the substring si…sj
is a
palindrome, and 0 otherwise.
To speed up the algorithm,
the values of IsPal(i, j) are stored in the cells of a
two-dimensional array pal[i][j].
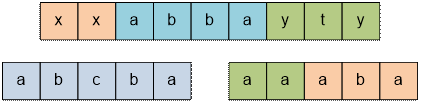
A string is called a superpalindrome
if it can be represented as a concatenation of one or more palindromes. For
example, the following strings are superpalindromes:
Let
![]()
Here it is assumed that i
< j, that is, the length of the substring is at least two.
Let us note the
base cases:
·
If i ≥ j, then the substring is either empty or
consists of a single character. Such strings are not considered palindromes by
definition. Therefore,
dp[i][j]
= 0 for i ≥ j
·
In particular, for any position i, we have dp[i][i]
= 0.
If the substring si…sj is a palindrome and
its length is at least two, then it is automatically a superpalindrome (since
it consists of a single palindrome). Therefore, for all pairs of indices (i, j) where 0 ≤ i < j < n, if the substring si…sj is a palindrome, we
can immediately set dp[i][j] = 1.
Now consider the general
case. Let the substring si…sj
not be a
palindrome as a whole. It can still be a superpalindrome if it can be split
into two parts, each of which is a superpalindrome.
To do this, iterate over
all possible split positions k such that i < k < j – 1.
The restriction k < j – 1 ensures that both substrings
si…sk
and sk+1…sj
have length at least two,
and therefore can potentially be superpalindromes.
If, for some k, the following conditions are satisfied:
·
dp[i][k] = 1,
·
dp[k + 1][j] = 1,
then the substring si…sj
can be
represented as a concatenation of two superpalindromes. Therefore, it is itself
a superpalindrome, and we set dp[i][j] = 1.

If this condition is not
satisfied for any valid k, then dp[i][j] remains 0.
Finally, count the number
of pairs (i, j) for which i < j and dp[i][j]
= 1. This
count is exactly the number of substrings of the string s that are
superpalindromes.
Example
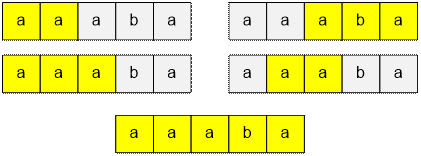
For the given example – the string “abacdc” – there are 3 substrings
that are superpalindromes:
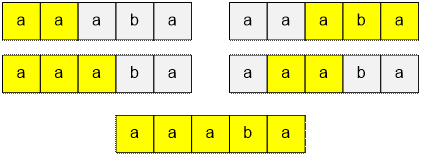
For the string “aaaba”,
there are 5 substrings that are superpalindromes:
Algorithm implementation
Declare the arrays.
#define MAX 1010
char s[MAX];
int dp[MAX][MAX];
int pal[MAX][MAX];
The function IsPal(i, j)
checks
whether the substring si…sj is a palindrome. The substring si …
sj is a palindrome if si = sj and the substring si+1…sj-1 is also a palindrome. The values of the function IsPal(i, j)
are stored in
the cells of the two-dimensional array pal[i][j].
int IsPal(int
i, int j)
{
if (i >=
j) return pal[i][j] = 1;
if (pal[i][j]
!= -1) return pal[i][j];
return
pal[i][j] = (s[i] == s[j]) && IsPal(i + 1,j - 1);
}
The main part of the
program. Read the input string s and compute its length n.
cin >> s; n = s.size();
Initialize the arrays dp and pal.
memset(dp,0,sizeof(dp));
memset(pal,-1,sizeof(pal));
Iterate over all substrings si … si + len of the string s in increasing order of
their length len. This is important because the value of dp[i][j] depends on the
values for shorter substrings.
for (len = 1; len < n; len++)
for (i = 0; i + len < n; i++)
{
The right boundary of the substring si …
si + len is j = i + len.
j = i + len;
If the substring si…sj is a palindrome, then it is
automatically also a superpalindrome.
if
(IsPal(i,j))
{
dp[i][j] = 1;
continue;
}
If the substring si…sj is not a
palindrome, we try to represent it as a concatenation of two superpalindromes.
If si…sk
and sk+1…sj are superpalindromes, then si…sj is a superpalindrome as well.
for (k = i + 1; k
< j - 1; k++)
if (dp[i][k]
&& dp[k + 1][j])
{
dp[i][j] = 1;
break;
}
}
Count the number of superpalindromes. It is equal to the number of index
pairs (i, j) for which dp[i][j] = 1.
res = 0;
for (i = 0; i < n; i++)
for (j = i + 1; j < n;
j++)
res += dp[i][j];
Print the answer.
printf("%d\n",res);
Algorithm implementation – recursion
Declare the input string s and arrays.
#define MAX 1010
string s;
int dp[MAX][MAX], pal[MAX][MAX];
The function IsPal(i, j)
checks
whether the substring si…sj is a palindrome. The substring si …
sj is a palindrome if si = sj and the substring si+1…sj-1 is also a palindrome. The values of the function IsPal(i, j)
are stored in
the cells of the two-dimensional array pal[i][j].
int IsPal(int
i, int j)
{
if (i >=
j) return pal[i][j] = 1;
if (pal[i][j]
!= -1) return pal[i][j];
return
pal[i][j] = (s[i] == s[j]) && IsPal(i+1,j-1);
}
The function f(i, j) returns 1 if the substring si…sj
is a
superpalindrome.
int f(int
i, int j)
{
A superpalindrome must contain more than one character.
if (i == j) return dp[i][j] = 0;
If the value of f(i,
j) is already computed, return this
value.
if (dp[i][j]
!= -1) return dp[i][j];
If the substring si…sj (i < j) is a palindrome, then it
is also a superpalindrome.
if
(IsPal(i,j)) return dp[i][j] = 1;
If the substring si…sk
(i < k) is a palindrome and the
substring sk+1…sj (k + 1 < j) is a
superpalindrome, then the substring si…sj is a superpalindrome.
for (int k = i + 1; k < j - 1; k++)
if (IsPal(i,k)
&& f(k + 1,j)) return dp[i][j] = 1;
If none of the conditions described above is satisfied, then the substring
si…sj is not a superpalindrome.
return
dp[i][j] = 0;
}
The main part of the
program. Read the input string s and compute its length n.
cin >> s; n = s.size();
Initialize the arrays dp and pal.
memset(dp,-1,sizeof(dp));
memset(pal,-1,sizeof(pal));
In the variable res count the number of superpalindromes.
res = 0;
for (i = 0; i <
n; i++)
for (j = i + 1; j
< n; j++)
res += f(i,j);
Print the answer.
cout << res << endl;
Java implementation
import java.util.*;
public class Main
{
static
String s;
static int dp[][],
pal[][];
static int
IsPal(int i, int j)
{
if (i
>= j) return pal[i][j] =
1;
if (pal[i][j] !=
-1) return pal[i][j];
if (s.charAt(i) == s.charAt(j)
&& IsPal(i+1,j-1)
== 1) pal[i][j] =
1;
else pal[i][j] =
0;
return pal[i][j];
}
static int f(int i, int j)
{
if (i == j) return dp[i][j] =
0;
if (dp[i][j] !=
-1) return dp[i][j];
if (IsPal(i,j) == 1) return dp[i][j] =
1;
for(int k = i + 1;
k < j - 1; k++)
if(IsPal(i,k) == 1
&& f(k + 1,j) ==
1) return dp[i][j] =
1;
return dp[i][j] =
0;
}
public static void
main(String[] args)
{
Scanner con = new
Scanner(System.in);
s = con.nextLine();
int n = s.length();
dp = new int[n][n];
pal = new int[n][n];
for(int i = 0;
i < n; i++)
for(int j = 0;
j < n; j++)
{
dp[i][j] =
-1;
pal[i][j] =
-1;
}
int res = 0;
for(int i = 0;
i < n; i++)
for(int j = i+1; j <
n; j++)
res += f(i,j);
System.out.println(res);
con.close();
}
}